METAL OXIDE SEMICONDUCTOR (MOS) TRANSISTOR

Metal Oxide Semiconductor structure

*        The structure consist of three layers: the metal gate electrode, the insulating oxide (SiO2) layer, and the p-type bulk semiconductor (Si), called the substrate.

*        The MOS structure forms a capacitor, with the gate and the substrate acting as the two terminals (plate) and the oxide layer as the dielectric.

*        The thickness of the silicon dioxide layer is usually between 10nm and 15nm.

Two terminal MOS structure

*        Consider basic electric properties of semiconductor (Si) substrate, which acts as one of the electrodes of MOS capacitor.

*        The equilibrium concentrations of mobile carriers in a semiconductor always obey the Mass Action Law given by

                       n.p = ni²

here, n and p denote the mobile carrier concentration of   electrons and holes respectively, and ni denotes the intrinsic carrier concentration of silicon.

*        At room temperature, i.e., T=300K, ni is approximately equal to 1.45 × 10^10 cm-³

*        Assuming that the substrate is uniformly doped with an acceptor concentration NA, the equilibrium electron and hole concentration in the p-type substrate are approximated by

Npo ~= ni² / NA

Npo ~= NA

The order of the doping concentration NA is typically 10^15 to 10^16 cm-³; thus it is much greater than the intrinsic carrier concentration ni.

The Fermi Potential ᵩF

*        The Fermi potential ᵩF, which is a function of temperature and doping, denotes the difference between the intrinsic Fermi level E_i, and the Fermi level E_F.

ᵩF = (E_F – E_i)/q    .......... (1)

For p-type semiconductor, the Fermi potential can be approximated by

ᵩFP = (KT/q)ln(n_i/N_A)    ……………………(2)

Whereas for an n-type semiconductor (doped with a donor concentration N_D), the Fermi potential is given by

ᵩFN = (KT/q)ln(N_D/n_i)   ……………………(3)

Here, K denotes the Boltzmann constant and q denotes the unit charge.

*        Note that the definitions given in (2) and (3) result in a positive Fermi potential for n-type material, and a negative Fermi potential for p-type material.

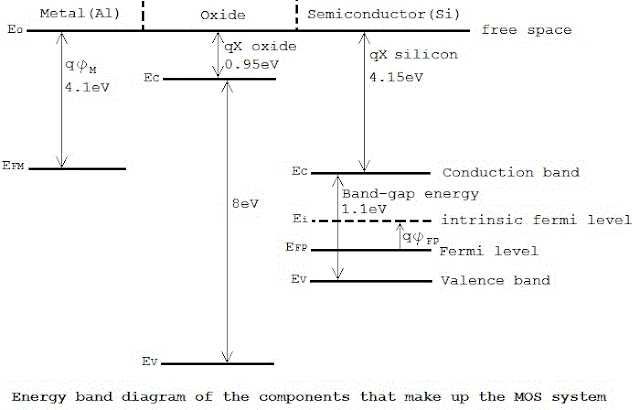
*        The electron affinity of silicon is denoted by qX.

*        The energy required for an electron to move from the Fermi level into free space is called the work function qᵩ_s, and is given by

       qᵩ_s = qX + (E_C – E_F)    ……………… (4)

*        The insulting silicon diaoxide layer between the silicon substrate and the gate has a large band gap of about 8eV and an electron affinity of about 0.95eV.

*        On the other hand, the work function qᵩ_M of an aluminium gate is about 4.1eV.

*        Now consider that the three components of the ideal MOS system are brought into the physical contact.

*        Because of work function difference between the metal and the semiconductor, a voltage drop occurs across the MOS system. Part of this built-in voltage drop occurs across the insulating oxide layer. The rest of the voltage drop occurs at the silicon surface next to the silicon oxide interface, forcing the energy bands of silicon to bend in this region.

*        The Fermi potential at the surface, also called surface potential ᵩ_s, is smaller in magnitude than the bulk Fermi potential ᵩ_F.

The MOS system under External Bias

*        Assume that the substrate voltage is set at V_B = 0, and let the gate voltage be the controlling parameter. Depending on the polarity regions can be observed for the MOS system: Accumulation, Depletion and Inversion.

 i.     Accumulation:

             *        If a negative voltage V_G is applied to the gate electrode,      the holes in the p-type substrate are attracted to the  semiconductor-oxide interface. The majority carrier concentration near the surface becomes larger than the equilibrium hole concentration in the substrate; hence, this condition is called carrier accumulation on the surface.

*        Note that in this case, the oxide electric field is directed      towards the gate electrode. That negative surface potential also  causes the energy bands to bend upward near the surface increases  as a result of the applied negative gate bias, the electron  concentration decreases as the negatively charged electrons are  pushed deeper into the substrate.

 ii.     Depletion: 

*         Consider a small positive gate bias VG is applied to the gate electrode. Since the substrate bias is zero, the oxide electric field will be directed towards the substrate. In this case, the positive surface potential causes the energy bands to bend downward near the surface.

*        The majority carrier, i.e., the holes in the substrate, will be repelled back into the substrate as a result of the positive gate bias, and these holes will leave negatively charged fixed acceptor ions behind. Thus, a depletion region is created near the surface.

Depth of depletion region

*        The thickness xd of the depletion region on the surface can easily be found as a function of the surface potential ᵩ_s.

*        Assume that the mobile hole charge in a thin horizontal layer parallel to the surface is

    dQ = -q.N_A.dx       …………… (1)

*        The change in surface potential can be found by using the poisson equation

*        Integrating (2) along the vertical dimesion (perpendicular to the surface) yields

*        Thus, the depth of the depletion region is

and the depletion region charge density, which consists solely of fixed acceptor ions in this region, is given by the following expression

Q = -q.N_A.x_d = -√(2q.N_A.ε_Si.|ᵩ_s - ᵩ_F|) ……………(6)

       iii.     Inversion

*        Consider a further increase in the positive gate bias. As a result of the increasing surface potential, the downward bending of the energy bands will increase as well.

*        Eventually, the mid-gap energy level E_i becomes smaller than the Fermi level E_FP on the surface, which means that the substrate semiconductor in the region becomes n-type.

*        Within this thin layer, the electron density is larger than the majority hole density, since the positive gate potential attracts additional minority carriers (electron) from the bulk substrate to the surface.

*        The n-type region created near the surface by the positive gate bias is called inversion layer, and this condition is called surface inversion.

*        The surface is said to be inverted when the density of mobile electrons on the surface becomes equal to the density of holes in the bulk (p-type) substrate. This condition requires that the surface potential has the same magnitude, but the reverse polarity, as the bulk Fermi potential ᵩ_F.

*        Once the surface is inverted, any further increase in the gate voltage leads to an increase of mobile electron concentration on the surface, but not to an increase of the depletion depth. Thus, the depletion region depth achieved at the onset of surface inversion is also equal to the maximum depletion depth, x_dm, which remains constant for higher gate voltages. Using the inversion condition ᵩ_S = -ᵩ_F, the maximum depletion region depth at the onset of surface inversion can be found as follows:

x_dm = √(2.ε_Si.|2ᵩ_F|/q.N_A)